
퀵정렬 알고리즘이란?
하나의 기준점을 가지고 분할과 정복 방식으로 정렬하는 알고리즘이다. 최선의 경우 O(NlogN) 의 속도를 낼 수 있다.
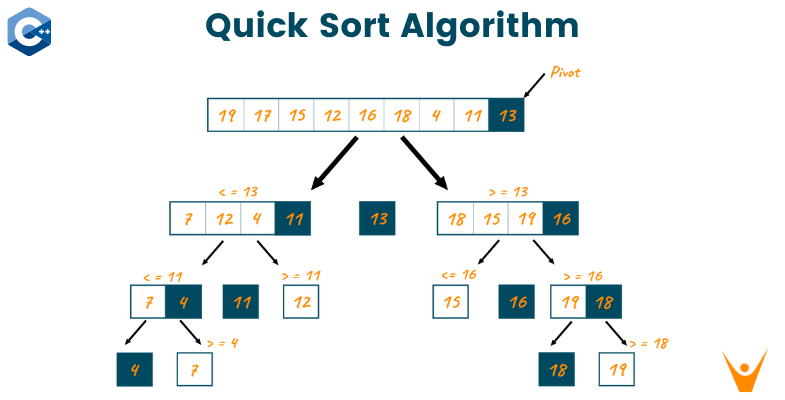
아래 그림에서는 가장 오른쪽에 위치한 요소를 첫 번째 피봇 기준점으로 삼았지만, 전체 배열의 중간 요소를 초기 시작점으로 정하는 것이 일반적이다.
처음 정한 피봇을 기준으로 전체 배열 안에서 피봇의 위치를 확정할 수 있는데, 이 때 정렬은 피봇을 기준으로 좌측에 순서 상관 없이 피봇보다 작은 값, 우측으로 순서 상관 없이 피봇보다 큰 값이기 때문에 피봇에 대한 위치는 확정적이라고 할 수 있다.
한 번의 반복이 끝나면 피봇의 위치가 확정되고, 이 피봇의 위치를 기준으로 좌측, 우측이 분할되기 때문에 각 범위를 다시 재귀적으로 호출하여 최종적으로 정렬할 범위 안에 요소가 1개가 남을 때까지 반복해준다.
퀵정렬 알고리즘 코드 적용
function quickSort(items) {
// 첫 실행 : 정렬 함수에 배열과 left, right 인덱스를 전달하여 호출한다.
return quickSortHelper(items, 0, items.length - 1);
}
function quickSortHelper(items, left, right) {
// 재귀 탈출 조건 :정렬 범위가 좁혀지면서 left가 right 를 넘어가는 시점에 종료한다.
if (left >= right) return;
// partition 함수를 호출해 정렬이 완료된 기준점을 반환받는다.
let index = partition(items, left, right);
// 정렬이 완료된 index 기준 더 작은 범위를 재귀적으로 호출하여 정렬
quickSortHelper(items, left, index - 1);
// index 기준 더 큰 범위를 재귀적으로 호출하여 정렬
quickSortHelper(items, index, right);
return items;
}
// 정렬이 완료된 기준점을 반환할 함수
function partition(array, left, right) {
// 피봇의 위치를 현재 범위(left ~ right) 의 중앙으로 잡는다.
let pivot = array[Math.floor((left + right) / 2)];
// left가 right보다 작은 동안 계속 반복한다.
while (left <= right) {
// 현재 피봇이 배열의 left 보다 크다면 left 포인터를 오른쪽으로 이동시킨다.(left < pivot)
while (pivot > array[left]) {
// pivot 보다 큰 값을 가리키거나, (pivot 기준 왼쪽이 다 작은 경우) pivot을 가리키게 된다.
left++;
}
// 현재 피봇이 배열의 right보다 작다면 right 포인터를 왼쪽으로 이동시킨다. (pivot < right)
while (pivot < array[right]) {
// pivot 보다 작은 값을 가리키거나, pivot을 가리키게 된다.
right--;
}
// left와 right 의 위치를 서로 swap 하고, left와 right를 하나씩 증가시킨다.
// left와 right가 각각 피봇보다 큰 값, 피봇보다 작은 값을 가리키므로
// 피봇을 기준으로 좌측이 작은 값, 우측이 큰 값이 되도록 자리를 교환한다.
if (left <= right) {
[array[left], array[right]] = [array[right], array[left]];
left++;
right--;
}
}
// 모든 반복이 끝나면 피봇의 위치는 확정되고, 피봇을 가리키는 left 를 리턴한다.
return left;
}
console.log(quickSort([6, 1, 23, 4, 2, 3]));참고자료
'Algorithm & 자료구조 > 자료구조' 카테고리의 다른 글
| [알고리즘 JS] 삽입 정렬 알고리즘 : Insertion Sort Algorithm (0) | 2022.10.01 |
|---|---|
| [알고리즘 JS] 버블 정렬 알고리즘 : Bubble Sort Algorithm (0) | 2022.08.31 |
| [알고리즘 JS] 이진 검색 알고리즘 : Binary Search Algorithm (0) | 2022.07.26 |
| [알고리즘 JS] 선택 정렬 알고리즘 : Selection Sort Algorithm (0) | 2022.07.22 |
![[알고리즘 JS] 퀵정렬 알고리즘 : Quick Sort Algorithm](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FPQbQ4%2FbtrN9rQkUZE%2FAAAAAAAAAAAAAAAAAAAAAI7BgJZkeNrijbzTbInustltfDtdJ78qgXxmwm7h0sbW%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3Dl7kTHpJMtqSLaF66QhJFOshxat8%253D)